We can use the GNU Octave tool to acquire samples from the RedPitaya and then do basically whatever processing we want.
The function acquire shown below is a simple GNU Octave script that loads samples from the RedPitaya and returns the sample vectors as a two-column matrix. As input it needs the RedPitaya IP address, the number of samples to acquire (max. 16384), the optional decimation factor and averaging selection.
As I’m running Octave on windows the PuTTy tool must also be installed to be able to transfer data over an SSH connection.
%> @brief Acquire samples from Red Pitaya.
%>
%> Note: PuTTy must be installed and the path to the PuTTY
%> installation folder must be in included into the windows
%> search path.
%>
%> @param ipAddress Red Pitaya IP address (or hostname).
%> @param nSamples Number of samples to capture.
%> @param decimationFactor Decimation factor (1,8,64,1024,8192,65536).
%> @param averagingIsEnabled If true, enable averaging when decimating.
%> @retval data Acquired data (two columns, channels 1 and 2).
function data=acquire(ipAddress,nSamples,decimationFactor,averagingIsEnabled)
DATA_FILE = 'data.txt';
if puttyIsNotInstalled
disp('plink.exe not found, please install PuTTy!');
return
end
setAveragingRegister(ipAddress, averagingIsEnabled);
acquireDataIntoFile(ipAddress,DATA_FILE,nSamples,decimationFactor);
data = loadDataFromFile(DATA_FILE);
deleteFile(DATA_FILE);
end
function notInstalled = puttyIsNotInstalled
status = dos('where /Q plink.exe');
notInstalled = (status>0);
end
function setAveragingRegister(ipAddress, averagingIsEnabled)
REG_ADDRESS='0x40100028';
regValue = '0x0';
if averagingIsEnabled
regValue = '0x1';
end
rpCommand = ['/opt/bin/monitor ',REG_ADDRESS,' ',regValue];
winCommand=['plink -l root -pw root ',ipAddress,' "',rpCommand,'"'];
disp('- set the averaging FPGA register'); fflush(stdout);
dos(winCommand);
end
function acquireDataIntoFile(ipAddress,dataFile,nSamples,decimationFactor)
rpCommand = ['/opt/bin/acquire ',num2str(nSamples),' ',num2str(decimationFactor)'];
winCommand=['plink -l root -pw root ',ipAddress,' "',rpCommand,'"',' > ', dataFile];
disp("- acquire data"); fflush(stdout);
dos(winCommand);
end
function data = loadDataFromFile(fileName)
data=load(fileName);
end
function deleteFile(fileName)
dos(['del ',fileName]);
end
As an example let’s see how the acquire function can be used to measure the signal-to-noise ratio (SNR) of a captured signal.
The main function is called analyzeSNR (shown below). It first acquires samples from the RedPitaya by calling the acquire function (line 10). It then plots the sample vector, calls the calculateSNR function and finally annotates the returned SNR value to the plot.
The functions calculateSNR and annotatePlot can be saved into the same source file (analyzeSNR.m). The calculateSNR function could also be saved into a separate .m file so that it can be called from other .m files.
CalculateSNR calls the sinefit function to fit a sine wave to the acquired data (using a least squares method) and returns the sine wave (signal) parameters and information about the residual (noise) signal.
The SNR can then be calculated from the equation:
As input to sinefit we just enter the acquired samples vector (data), the time vector (t) and the estimated sine wave frequency (freq).
[params,yest,yres,rmserr] = sinefit(data,t,freq,verbose,plot_flag);
The returned parameters are described in the table below.
| params(1) | Estimated sine wave DC offset. |
| params(2) | Estimated sine wave amplitude. |
| params(3) | Estimated sine wave frequency in Hz. |
| params(4) | Estimated sine wave phase in radians. |
| yest | Estimated sine wave vector. |
| yres | Residual signal vector. |
| rmserr | RMS of the residual signal. |
function analyzeSNR
close all
ipAddress = "redpitaya";
nSamples = 16384;
decimationFactor = 1;
averagingIsEnabled = 0;
data=acquire(ipAddress,nSamples,decimationFactor,averagingIsEnabled);
fprintf("Acquired %d samples\n",length(data));
freq = 20e3;
sampleRate = 125e6;
for channelNumber=1:2
figureId = figure;
plot(data(:,channelNumber));
grid
[SNR,offset,amplitude,freqHz,angleRad] = ...
calculateSNR(data(:,channelNumber),freq,sampleRate);
annotatePlot(figureId,channelNumber,SNR,offset,amplitude,freqHz,angleRad);
end
end
function [SNR,offset,amplitude,freqHz,angleRad] = ...
calculateSNR(data, freq, sampleRate)
Ts = 1/sampleRate;
N = numel(data);
t=(0:N-1)*Ts;
verbose = 0;
plot_flag = 0;
[params,yest,yres,rmserr] = sinefit(data,t,freq,verbose,plot_flag);
offset = params(1);
amplitude = params(2);
freqHz = params(3);
angleRad = params(4);
rmssig = amplitude/sqrt(2);
SNR = 20*log10(rmssig/rmserr);
end
function annotatePlot(figId,channelNumber,SNR,offset,amplitude,freqHz,angleRad)
figure(figId);
title(sprintf('Channel %d: SNR = %.2f dB',channelNumber,SNR));
a=axis();
text(a(2),a(3),...
sprintf('amplitude = %.2f\n...
offset = %.2f\n
frequency = %.2f kHz\n
phase = %.1f degrees',...
amplitude, offset, freqHz/1e3, angleRad/2/pi*360),...
'verticalAlignment','bottom',...
'horizontalAlignment','right');
end
The sinefit function can be obtained from the Mathworks File Exchange (the code is covered by the BSD License):
http://www.mathworks.com/matlabcentral/fileexchange/23214-four-parameter-sinefit
The sinefit function was originally written for MATLAB but with a couple of simple changes I managed to get it running on Octave, too.
I’ll enclose the modified source code here.
Maybe we should also check how well the sinefit method can estimate the SNR. Let’s create a small test bench for evaluating the estimation accuracy. The idea here is to create a known sine signal and a known noise signal so that we know the exact SNR and then sum up the two signals and use the sinefit function to estimate the SNR.
function tb_sinefit
close all
sampleRate=125e6;
Ts=1/sampleRate;
nSamples=16384;
t=(0:nSamples-1)*Ts;
f=20e3;
% reference signal
signal=real(exp(1j*2*pi*f*t));
rmsSignal=rms(signal);
nMeasurements = 50;
for iMeasurement=1:nMeasurements
noiseLevel=0.00025*iMeasurement;
% reference noise
noise=noiseLevel*randn(1,nSamples);
rmsNoise=rms(noise);
% reference SNR
refSNR(iMeasurement) = 20*log10(rmsSignal/rmsNoise);
% estimate SNR from the noisy signal
noisySignal = signal + noise;
measuredSNR(iMeasurement) = ...
calculateSNR(noisySignal, f, sampleRate);
end
compareSNR(refSNR,measuredSNR);
end
function compareSNR(refSNR,measuredSNR)
subplot(2,1,1)
plot(refSNR,'bo')
hold on
plot(measuredSNR,'r.')
legend('reference','measured')
grid
ylabel('SNR [dB]')
xlabel('Measurement number')
title('sinefit accuracy')
subplot(2,1,2)
difference = refSNR-measuredSNR;
plot(difference,'bx');
grid
ylabel('Difference [dB]')
xlabel('Measurement number')
minDiff = floor(min(difference)*100)/100;
maxDiff = ceil(max(difference)*100)/100;
a = axis;
axis([a(1:2) minDiff maxDiff])
end
function y = rms(x)
y = norm(x)/sqrt(length(x));
end
The results are shown below. The estimated SNR is very close to the reference value. The difference is about 0.13dB (looks like the estimated SNR is consistently slightly smaller than the actual value).
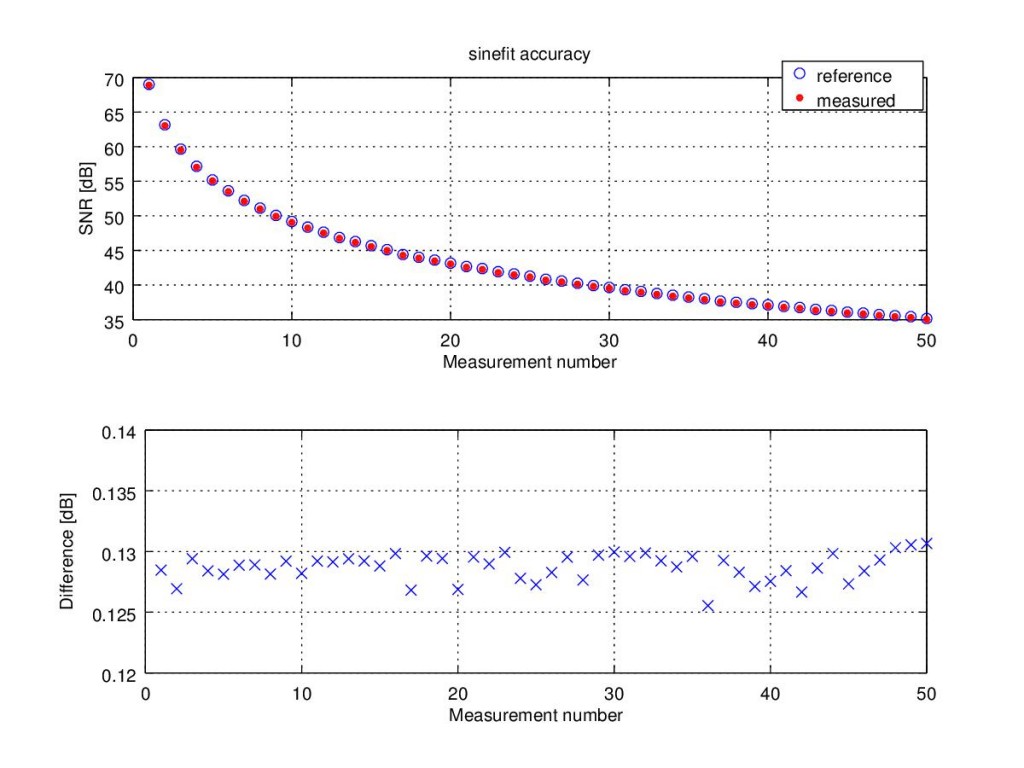
It’s not SNR but SINAD!
Cordially